Multi-modal analysis of aerosol robotic network size distributions for remote sensing applications - dominant aerosol type cases
Abstract
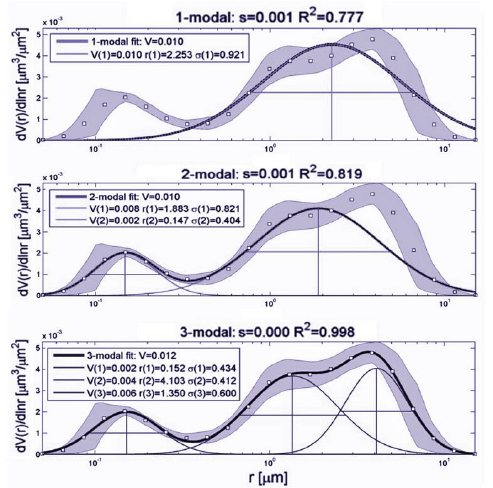
To date, size distributions obtained from the aerosol robotic network (AERONET) have been fit with bi-lognormals defined by six secondary microphysical parameters - the volume concentration, effective radius, and the variance of fine and coarse particle modes. However, since the total integrated volume concentration is easily calculated and can be used as an accurate constraint, the problem of fitting the size distribution can be reduced to that of deducing a single free parameter - the mode separation point. We present a method for determining the mode separation point for equivalent-volume bi-lognormal distributions based on optimization of the root mean squared error and the coefficient of determination. The extracted secondary parameters are compared with those provided by AERONET’s Level 2.0 Version 2 inversion algorithm for a set of benchmark dominant aerosol types, including desert dust, biomass burning aerosol, urban sulphate and sea salt. The total volume concentration constraint is then also lifted by performing multi-modal fits to the size distribution using nested Gaussian mixture models, and a method is presented for automating the selection of the optimal number of modes using a stopping condition based on Fisher statistics and via the application of statistical hypothesis testing. It is found that the method for optimizing the location of the mode separation point is independent of the shape of the aerosol volume size distribution (AVSD), does not require the existence of a local minimum in the size interval 0.439 μm < r < 0.992 μm, and shows some potential for optimizing the bi-lognormal fitting procedure used by AERONET particularly in the case of desert dust aerosol. The AVSD of impure marine aerosol is found to require three modes. In this particular case, bi-lognormals fail to recover key features of the AVSD. Fitting the AVSD more generally with multi-modal models allows automatic detection of a statistically significant number of aerosol modes, is applicable to a very diverse range of aerosol types, and gives access to the secondary microphysical parameters of additional modes currently not available from bi-lognormal fitting methods.