Abstract

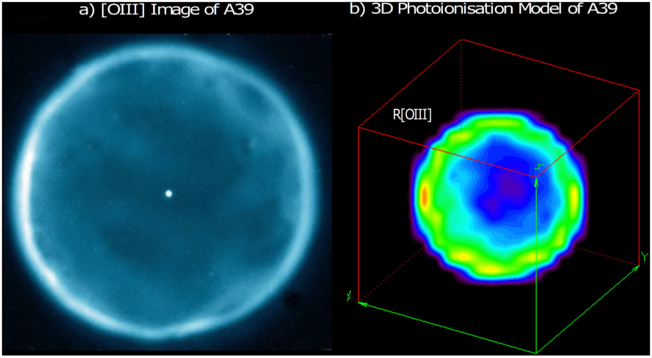
This tutorial presents a review of the analytical approach to obtain exact solutions for the populations of n-level ions, and summarizes the ideas behind detailed balance and the statistical physics of collisionally-excited ions. Seaton’s analytical solution for the populations of the 3-level ion has been supplanted by matrix methods such as the master equation approach, which are now central to astronomy since there is a need to maintain a parity between improvements in quantum-mechanically calculated values for collision strengths and transition probabilities on the one hand, and three-dimensional (3D) photoionization codes used by astrophysicists for producing nebular diagnostics on the other. We show that the analytical method of solution to the problem using matrices and symbolic mathematics is straightforward, and we illustrate through theoretical, numerical, and empirical checks the validity of its results. First, we recast the equations of thermal statistical equilibrium for the energy level populations of collisionally-excited ions in the form of a well-defined matrix equation. We then show how symbolic mathematics is efficient in the inversion of equations and is able to provide the exact analytical solutions for the sought-after level populations. We present the matrices for the 5-level ion as an example of how to extend the exact solution for the 3-level ion to illustrate the general technique. We then show how the analytical results faithfully reduce to the Seaton solution when appropriate limits are taken. Spectrophotometric observations of a real ionized gas (the planetary nebula A39) are then used to obtain empirical values of forbidden line ratios and level populations for the 5-level [O III] ion. These values are compared with - (1) a best-fit 3D Monte Carlo photoionization model, and (2) the exact solution for the 5-level ion, using the symbolic mathematics approach, the exact Seaton 3-level ion solution, and a numerical approximation for the 5-level ion. It is shown that in every case, the analytical solution agrees with results obtained using observed nebular conditions to within the standard error. We provide a MATLAB code that can be adapted and tailored by astrophysicists to calculations of other n-level ions.